|
|
|
\require{AMSmath}

Reageren...
Re: Extreempunten van rationale functie
Hallo,
Wij zijn bezig met een PO voor wiskunde, en we zitten met een vraag: Hoe bewijs je dat, in een boldriehoek, de som van de 3 hoeken altijd groter is dan 180 graden.
Dank u!
Antwoord
Even wat voorkennis:
Ik ga in dit bewijs werken met radialen. Ik neem aan dat je daar mee bekend bent.
Het overschot van de som van de hoeken boven p (=180į) wordt het exces genoemd. Oftewel in boldriehoek ABC:
exces = –A + –B + –C - p
Stelling:In een willekeurige boldriehoek met straal 1 is de oppervlakte gelijk aan het exces.
Deze gaan we bewijzen
Gegeven:
Boldriehoek ABC op een bol met r = 1
a = –BAC
b = –ABC
g = –ACB
Te bewijzen:
a + b + g = Opp(ABC) + p
Bewijs:
A' is het diametrale punt van A
B' is het diametrale punt van B
C' is het diametrale punt van C
NB: Het diametrale punt ligt precies aan de andere kant van de bol.
Voor de duidelijkheid even een figuur:
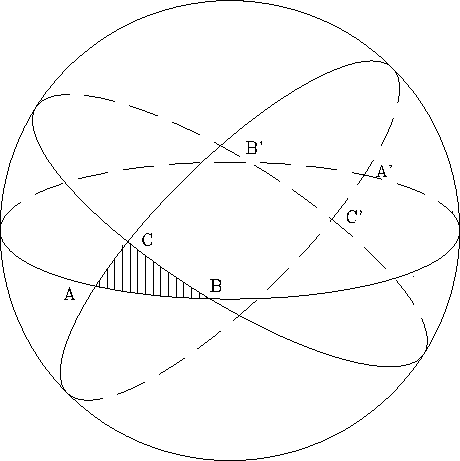
De boltweehoek AA', die je krijgt door boldriehoeken ABC en A'BC samen te nemen, is a/(2p)de deel van de bol.
Opp.(bol) = 4p
Opp.(boltweehoek AA') = 4p∑a/(2p) = 2a ř
Opp.(ABC) + Opp.(A'BC) = 2a
Analoog vinden we:
Opp.(ABC) + Opp.(AB'C) = 2b
Opp.(ABC) + Opp.(ABC') = 2g
Tel de formules bij elkaar op zodat je krijgt:
2a + 2b + 2g = 3∑Opp.(ABC) + Opp.(A'BC) + Opp.(AB'C) + Opp.(ABC')
Met behulp van puntsymetrie in het middelpunt van de bol kun je zien dat:
Opp.(ABC') = Opp.(A'B'C)
Je krijgt dan:
2a + 2b + 2g = 3∑Opp.(ABC) + Opp.(A'BC) + Opp.(AB'C) + Opp.(A'B'C)
Opp(ABC) + Opp(A'BC) + Opp(AB'C) + Opp(A'B'C) is nu de oppervlakte van de halve bol. En dus gelijk aan 2p. En dus geldt:
2a + 2b + 2g = 2∑Opp(ABC) + 2p
Aan beide kanten delen door twee geeft:
a + b + g = Opp(ABC) + p
Q.e.d
Waar het allemaal om te doen wasOmdat een boldriehoek altijd een (positieve) oppervlakte heeft volgt hier direct uit dat het exces (=hoekoverschot) postief is. En dus is de som van de drie hoeken van een boldriehoek altijd groter dan p.
Gebruik dit formulier alleen om te reageren op de inhoud van de vraag en/of het
antwoord hierboven. Voor het stellen van nieuwe vragen kan je gebruik maken
van een vraag stellen in het menu aan de linker kant. Alvast bedankt!
|


